You've Reached the Center of the Internet
It's a blog
Expected Outs Difference -- A simple team fielding metric
In this post, I’m going to outline a simple baseball team fielding metric I thought of. I’m calling it Expected Outs Difference or EOD.
Here’s the plan:
- Obtain a data set of balls put in play
- Train a supervised model to predict whether a given ball will become and out based on exit velocity, launch angle, and spray angle
- Evaluate a team’s defense by running the model against each ball they faced and comparing the predicted outs with the actual ones
This method allows me to compare how well a team’s defense does at compared to what we’d expect based on how other teams do.
The data
I started by downloading a 2023 Statcast dataset using pybaseball. This gave me a table containing every pitch from the season.
from pybaseball import statcast
from pybaseball.datahelpers.statcast_utils import add_spray_angle
OUTS_EVENTS = ["field_out", "fielders_choice_out", "force_out", "grounded_into_double_play", "sac_fly_double_play", "triple_play", "double_play"]
START_DATE = "2023-03-01"
END_DATE = "2023-10-01"
data = add_spray_anglestatcast(start_dt=START_DATE, end_dt=END_DATE))
# filter out strikes and balls
balls_in_play = data[data["type"] == "X"]
# filter out foul outs
balls_in_play = balls_in_play[balls_in_play["spray_angle"].between(-45, 45)]
# label outs
balls_in_play["out"] = balls_in_play["events"].isin(OUTS_EVENTS)
# drop rows with missing data
balls_in_play = balls_in_play.dropna(subset=["launch_angle", "launch_speed", "spray_angle"])
Statcast provides a lot of information, but what I most cared about was exit velocity, launch angle, spray angle, and play outcome.
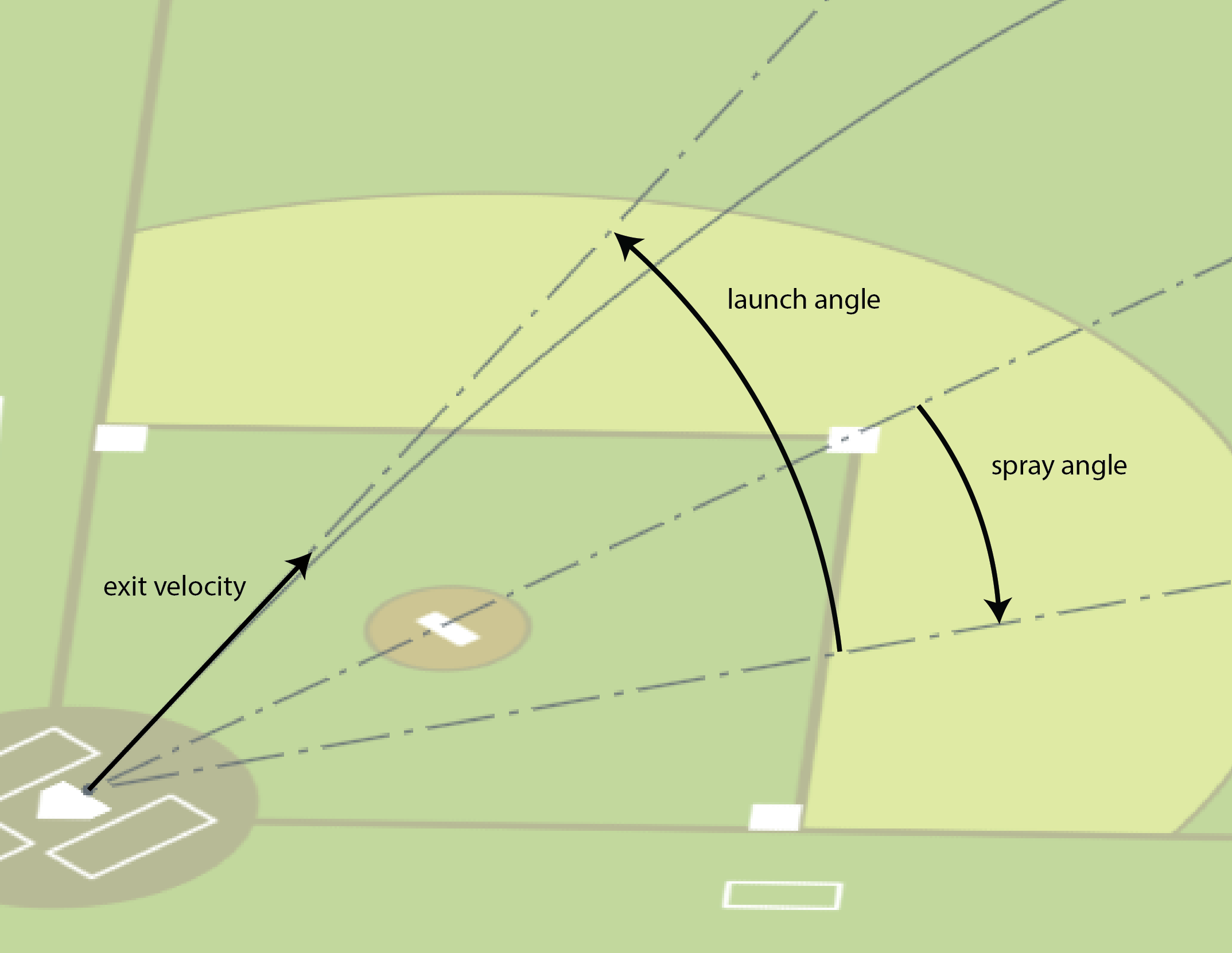
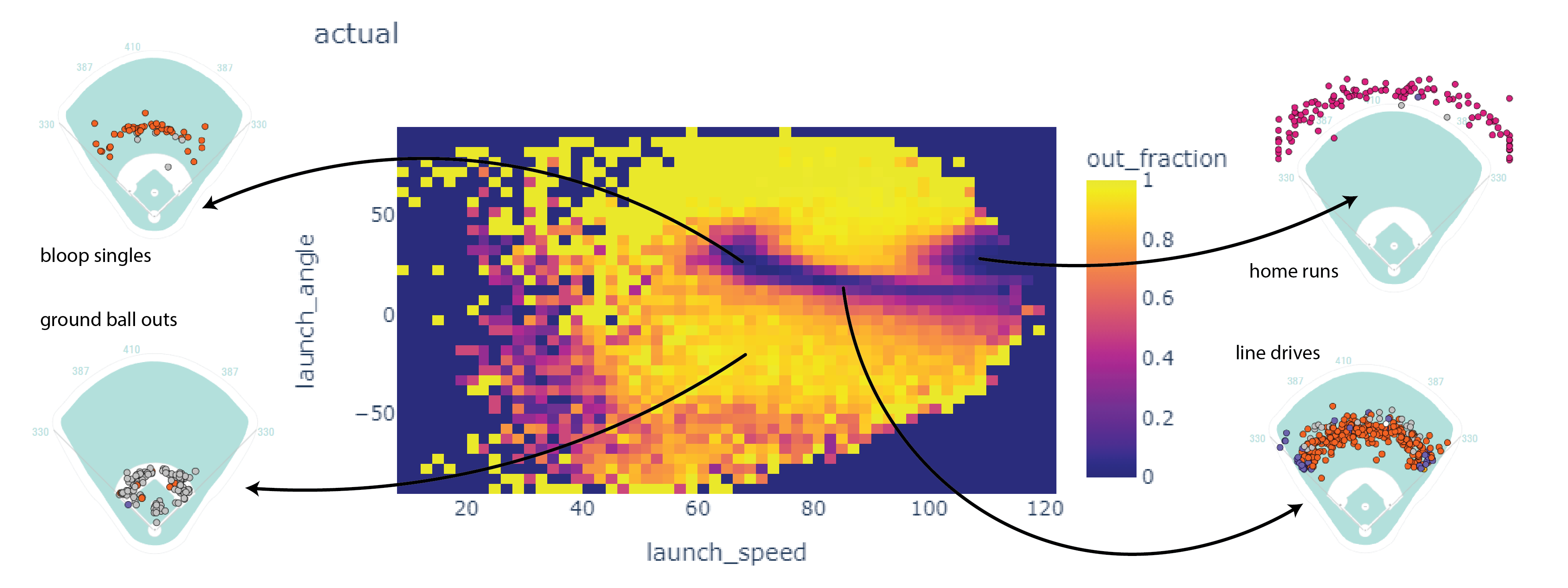
Here’s a 2D histogram showing the fraction of the hits within bins in exit velocity and launch angle that became outs.
Balls in the dark areas usually fall for hits.
Balls in the yellow areas are usually outs.
The model
I trained an SKLearn KNeighbors classifier. To make a prediction, this model looks up the eight most similar hits. If most of those hits became outs, the model classifies it as an out. If not, the model classifies it as a non-out.
from sklearn.neighbors import KNeighborsClassifier
X = balls_in_play[["launch_speed", "launch_angle", "spray_angle"]]
y = balls_in_play["out"]
clf = KNeighborsClassifier(n_neighbors=8).fit(X, y)
balls_in_play["predicted_out"] = clf.predict(X)
This isn’t perfect. When the model is classifying a point, it will always find the point itself as one of the nearest neighbors. I don’t think this is a big issue though.
Calculating EOD
Finally, I used the model to evaluate Expected Outs Difference.
# create a column giving the id of the fielding team
balls_in_play["fielding_team"] = np.where(balls_in_play["inning_topbot"] == "Top", balls_in_play["home_team"], balls_in_play["away_team"])
# group by fielding team and sum outs and predicted outs
teams = balls_in_play.groupby("fielding_team").agg({"out": "sum", "predicted_out": "sum", "events": "count"})
# subtracting the expected outs from the predicted outs gives Expected Outs Difference
teams["out_diff"] = teams["out"] - teams["predicted_out"]
teams.sort_values("out_diff", ascending=False)
out predicted_out events out_diff
fielding_team
MIL 2634 2561 3947 73
CHC 2622 2578 4057 44
BAL 2719 2679 4183 40
AZ 2787 2754 4309 33
TEX 2658 2626 4072 32
TOR 2702 2672 4204 30
SEA 2609 2580 3989 29
LAD 2729 2704 4144 25
CLE 2751 2730 4231 21
ATL 2581 2566 4035 15
KC 2688 2677 4272 11
SD 2565 2558 3919 7
DET 2783 2781 4310 2
CWS 2541 2539 4002 2
PIT 2766 2764 4350 2
MIN 2673 2677 4121 -4
NYM 2610 2619 4088 -9
NYY 2771 2780 4237 -9
TB 2719 2735 4146 -16
SF 2661 2681 4178 -20
WSH 2731 2754 4367 -23
MIA 2645 2669 4139 -24
HOU 2623 2649 4061 -26
OAK 2635 2667 4234 -32
STL 2922 2962 4660 -40
PHI 2772 2821 4301 -49
LAA 2620 2685 4153 -65
BOS 2633 2698 4179 -65
CIN 2636 2717 4179 -81
COL 2864 2957 4662 -93
Evaluating EOD against other fielding metrics
This approach seems to roughly match other popular fielding metrics.
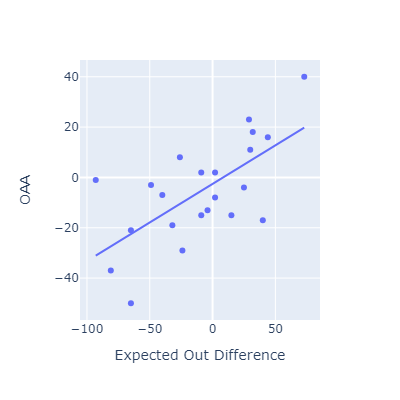
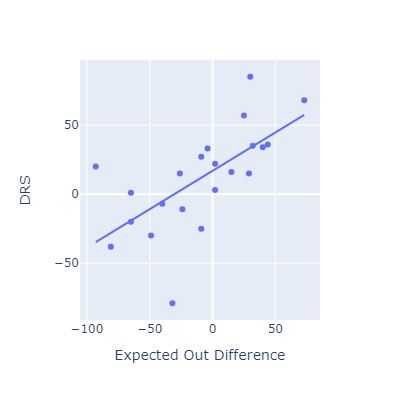
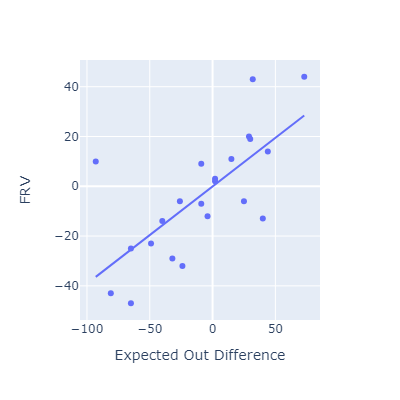
I think my method here is most conceptually similar to OAA. Oddly, that’s the metric that EOD correlates most poorly with.