In this post, I’m going to outline a simple baseball team fielding metric I thought of. I’m calling it Expected Outs Difference or EOD.

Here’s the plan:

• Obtain a data set of balls put in play
• Train a supervised model to predict whether a given ball will become and out based on exit velocity, launch angle, and spray angle
• Evaluate a team’s defense by running the model against each ball they faced and comparing the predicted outs with the actual ones

This method allows me to compare how well a team’s defense does at compared to what we’d expect based on how other teams do.

The data

I started by downloading a 2023 Statcast dataset using pybaseball. This gave me a table containing every pitch from the season.

from pybaseball import statcast
from pybaseball.datahelpers.statcast_utils import add_spray_angle

OUTS_EVENTS = ["field_out", "fielders_choice_out", "force_out", "grounded_into_double_play", "sac_fly_double_play", "triple_play", "double_play"]
START_DATE = "2023-03-01"
END_DATE = "2023-10-01"

data = add_spray_anglestatcast(start_dt=START_DATE, end_dt=END_DATE))

# filter out strikes and balls
balls_in_play = data[data["type"] == "X"]

# filter out foul outs
balls_in_play = balls_in_play[balls_in_play["spray_angle"].between(-45, 45)]

# label outs
balls_in_play["out"] = balls_in_play["events"].isin(OUTS_EVENTS)

# drop rows with missing data
balls_in_play = balls_in_play.dropna(subset=["launch_angle", "launch_speed", "spray_angle"])

Statcast provides a lot of information, but what I most cared about was exit velocity, launch angle, spray angle, and play outcome.

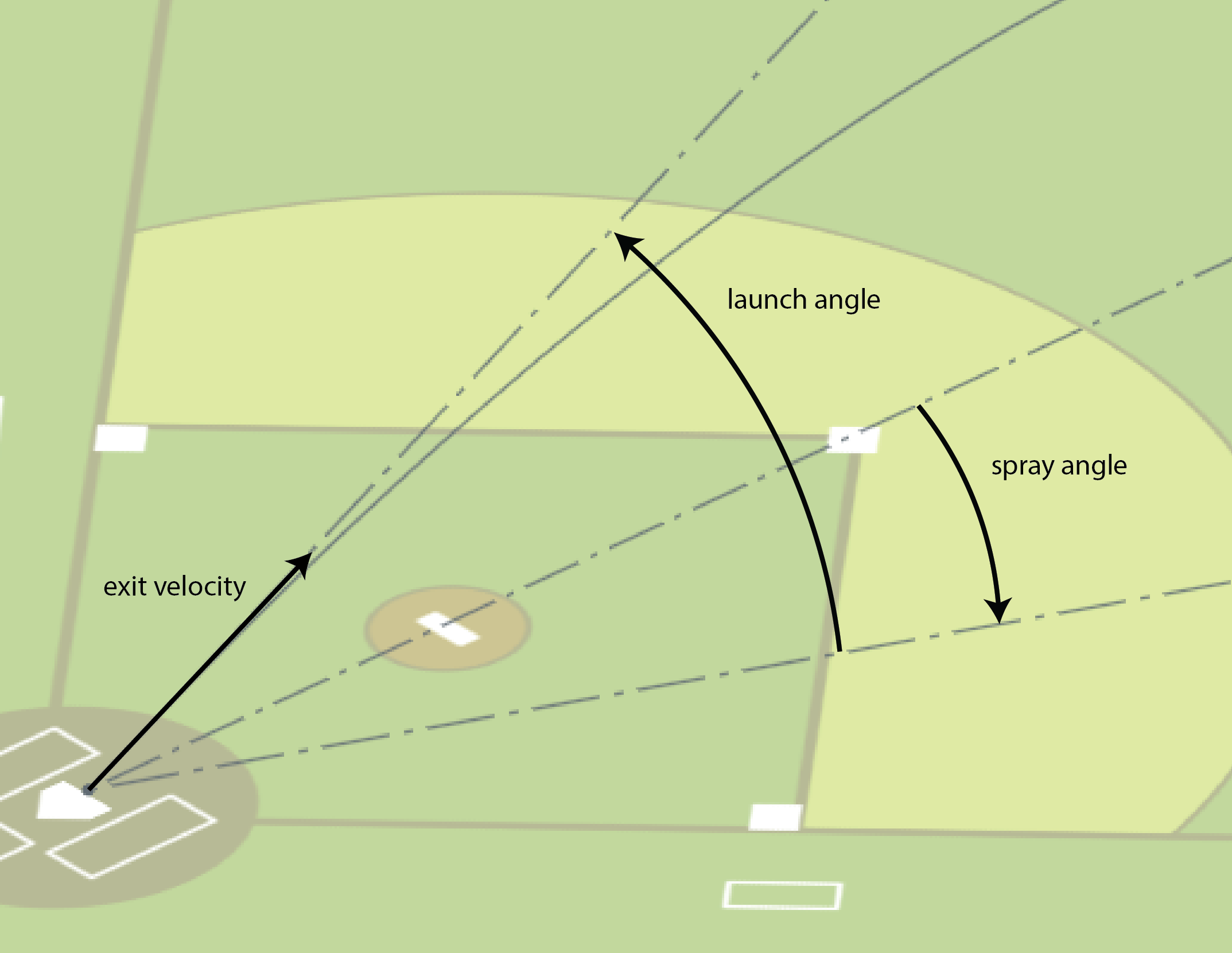
Here’s a 2D histogram showing the fraction of the hits within bins in exit velocity and launch angle that became outs. Balls in the dark areas usually fall for hits. Balls in the yellow areas are usually outs.

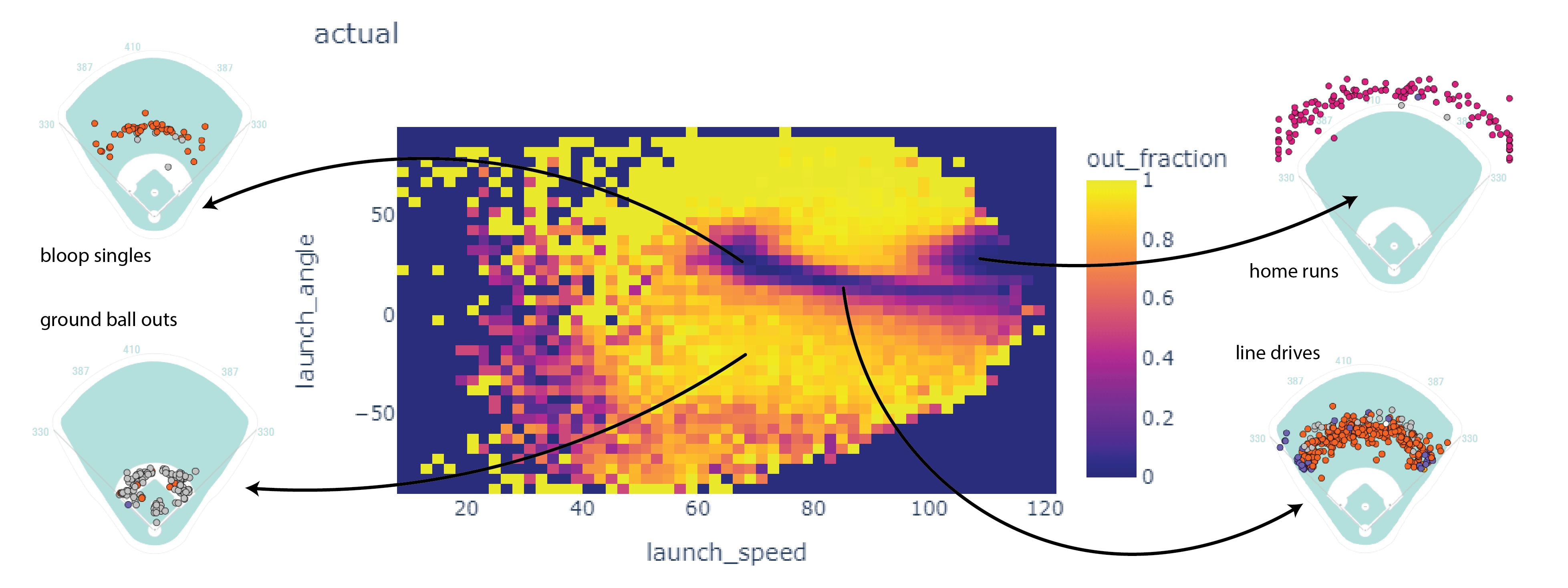
The model

I trained an SKLearn KNeighbors classifier. To make a prediction, this model looks up the eight most similar hits. If most of those hits became outs, the model classifies it as an out. If not, the model classifies it as a non-out.

from sklearn.neighbors import KNeighborsClassifier

X = balls_in_play[["launch_speed", "launch_angle", "spray_angle"]]
y = balls_in_play["out"]
clf = KNeighborsClassifier(n_neighbors=8).fit(X, y)

balls_in_play["predicted_out"] = clf.predict(X)

This isn’t perfect. When the model is classifying a point, it will always find the point itself as one of the nearest neighbors. I don’t think this is a big issue though.

Calculating EOD

Finally, I used the model to evaluate Expected Outs Difference.

# create a column giving the id of the fielding team
balls_in_play["fielding_team"] = np.where(balls_in_play["inning_topbot"] == "Top", balls_in_play["home_team"], balls_in_play["away_team"])

# group by fielding team and sum outs and predicted outs
teams = balls_in_play.groupby("fielding_team").agg({"out": "sum", "predicted_out": "sum", "events": "count"})

# subtracting the expected outs from the predicted outs gives Expected Outs Difference
teams["out_diff"] = teams["out"] - teams["predicted_out"]
teams.sort_values("out_diff", ascending=False)

              out	   predicted_out    events      out_diff
fielding_team				
MIL           2634          2561          3947          73
CHC           2622          2578          4057          44
BAL           2719          2679          4183          40
AZ            2787          2754          4309          33
TEX           2658          2626          4072          32
TOR           2702          2672          4204          30
SEA           2609          2580          3989          29
LAD           2729          2704          4144          25
CLE           2751          2730          4231          21
ATL           2581          2566          4035          15
KC            2688          2677          4272          11
SD            2565          2558          3919          7
DET           2783          2781          4310          2
CWS           2541          2539          4002          2
PIT           2766          2764          4350          2
MIN           2673          2677          4121          -4
NYM           2610          2619          4088          -9
NYY           2771          2780          4237          -9
TB            2719          2735          4146          -16
SF            2661          2681          4178          -20
WSH           2731          2754          4367          -23
MIA           2645          2669          4139          -24
HOU           2623          2649          4061          -26
OAK           2635          2667          4234          -32
STL           2922          2962          4660          -40
PHI           2772          2821          4301          -49
LAA           2620          2685          4153          -65
BOS           2633          2698          4179          -65
CIN           2636          2717          4179          -81
COL           2864          2957          4662          -93

Evaluating EOD against other fielding metrics

This approach seems to roughly match other popular fielding metrics.

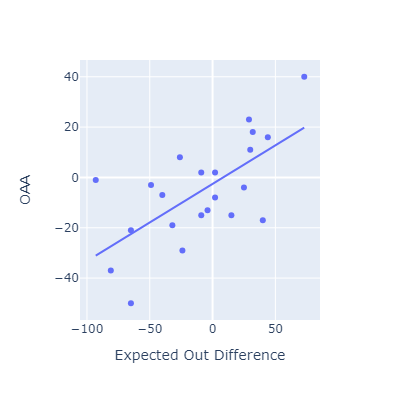
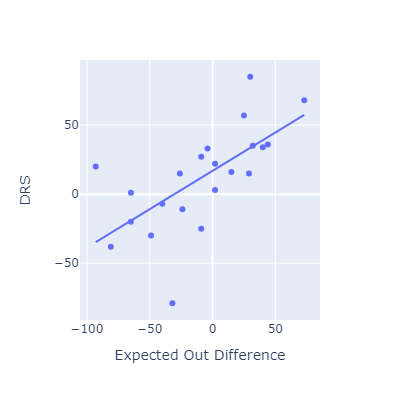
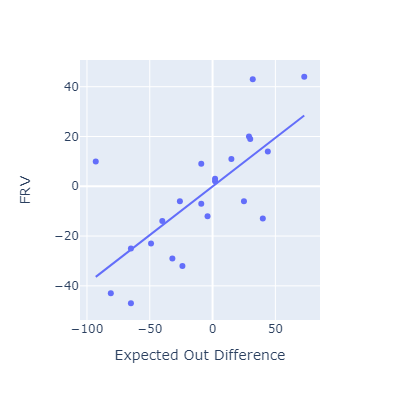
I think my method here is most conceptually similar to OAA. Oddly, that’s the metric that EOD correlates most poorly with.

Below is some simple code for building a run expectancy table based on Statcast data. A run expectancy table gives the average number of runs scored after each base/out state. For example, with runners on 1st and 2nd and one out, the table gives the average number of runs that scored.

import pandas as pd
from pybaseball import statcast


def run_expectancy(start_date: str, end_date: str) -> pd.Series:
    """
    Returns a run expectancy table based on Statcast data from `start_date` to `end_date`
    """
    pitch_data: pd.DataFrame = statcast(start_dt=start_date, end_dt=end_date)

    # create columns for whether a runner is on each base
    for base in ("1b", "2b", "3b"):
        pitch_data[base] = pitch_data[f"on_{base}"].notnull()

    pitch_data["inning_final_bat_score"] = pitch_data.groupby(
        ["game_pk", "inning", "inning_topbot"]
    )["post_bat_score"].transform("max")

    # filter down to one row per at-bat
    ab_data = pitch_data[pitch_data["pitch_number"] == 1]

    ab_data["runs_after_ab"] = (
        ab_data["inning_final_bat_score"] - ab_data["bat_score"]
    )

    # group by base/out state and calculate mean runs scored after that state
    return ab_data.groupby(["outs_when_up", "1b", "2b", "3b"])["runs_after_ab"].mean()

Here’s what it looks like for 2021:

print(run_expectancy("2021-04-01", "2021-12-01"))
---
outs_when_up  1b     2b     3b   
0             False  False  False    0.507303
                            True     1.393333
                     True   False    1.135049
                            True     2.107407
              True   False  False    0.916202
                            True     1.745745
                     True   False    1.523861
                            True     2.446313
1             False  False  False    0.264921
                            True     0.958691
                     True   False    0.684807
                            True     1.409165
              True   False  False    0.534543
                            True     1.126154
                     True   False    0.923244
                            True      1.68007
2             False  False  False    0.101856
                            True     0.385488
                     True   False    0.324888
                            True     0.600758
              True   False  False    0.228621
                            True     0.493186
                     True   False    0.451022
                            True     0.825928

If you’re a baseball fan, you’ll probably have come across a stat called FIP or Fielding Independent Pitching. As I understand it, FIP was designed by Tom Tango to track a pitcher’s peformance in a way that doesn’t depend on fielders or on which balls happen to fall between them or get caught. Because it removes these factors that are outside of a pitcher’s control, FIP is also said to me more stable year-to-year and to be a better measure of a pitcher’s skill.

I believe the theory behind this comes from work by Voros McCracken showing that pitchers don’t have much control over the fraction of balls put in play that fall for hits. This conflicts with some baseball common sense ideas like “pitching to contact”, but let’s leave that aside for now. The fraction of balls in play that become hits is sometimes called BABIP or Batting Average on Balls In Play. By diminishing the luck-based effects of BABIP, one can build a pitching statistic that’s more indicative of a pitcher’s true ability. That’s the idea.

To accomplish this goal, FIP is based on results that pitchers have the most control over: home runs, strikeouts, walks, and hit by pitch. Also, it’s constructed to have a similar scale to ERA to make it familiar to fans. Until recently, that was about all I knew.

It’s easy to find a formula online:

where \(\mathrm{HR}\), \(\mathrm{BB}\), \(\mathrm{HBP}\), \(\mathrm{SO}\), and \(\mathrm{IP}\) are the number of home runs, walks, hit by pitch, strike outs, and innings pitched collected by the pitcher, respectively. \(C_{\mathrm{FIP}}\) is a constant which varies year by year and is apparently usually around three. The constant brings FIP into the same range as ERA.

But where do the 13, 3, -2, and constant come from though? This is a bit harder to find.

In this post, I’ll derive a version of FIP in a way that makes sense to me. I’ll touch on this at the end, but I don’t think this is the way it’s actually done.

My method is simple: I trained a linear regression model to predict a pitcher’s ERA based on \(\mathrm{HR}\), \(\mathrm{BB} + \mathrm{HBP}\) and \(\mathrm{SO}\). FIP is just a linear combination of those parameters, so it will be easy to compare the trained parameters of the linear model with the real formula.

A look at the data

I used pybaseball to download full season pitching data from 2015 to 2023.

The relationships between the raw statistics are as you’d expect. For example, here’s ERA plotted against HR and SO: 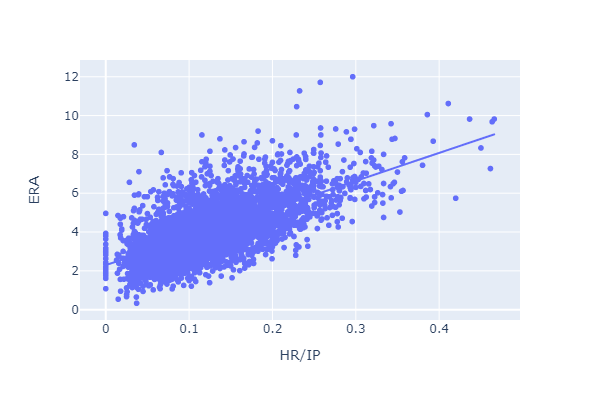Home runs allowed per inning pitched has a positive relationship with ERA.

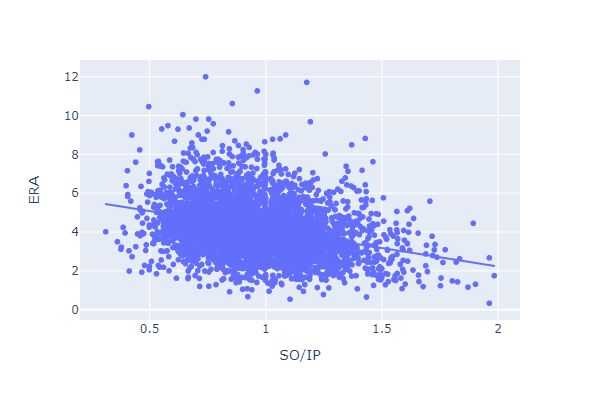Strikeouts per inning has a negative relationship with ERA. Let’s move on.

Training a linear model

Training a linear model is pretty easy:

from pybaseball import pitching_stats
from sklearn.linear_model import LinearRegression

logs = pitching_stats(2021, 2023, qual=25)

logs["UBB"] = logs["BB"] - logs["IBB"] # unintentional walks is total walks minus intentional walks
logs["UBB_HBP"] = logs["UBB"] + logs["HBP"] # sum walks and hit by pitch

X = logs[["HR", "UBB_HBP", "SO"]].div(logs["IP"], axis=0) # normalize by innings pitched
y = logs["ERA"]
weight = logs["IP"]
fip_reg = LinearRegression().fit(X, y, sample_weight=weight)

Two things to point out here:

1. I excluded pitchers with less than 25 innings pitched using the qual kwarg in the pitching_stats() call.
2. I weighted the samples based on innings pitched using sample_weight.

The relationship between ERA and FIP looks reasonable:

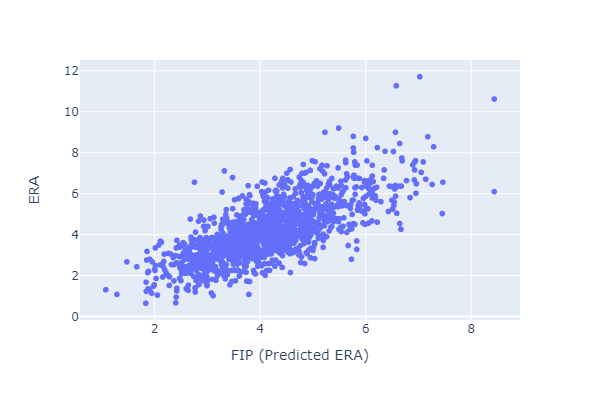
Here are the fitted parameters:

fip_reg.coef_, fip_reg.intercept_
> (array([13.28482645,  3.2804091 , -1.78295967]), 2.8140810888761045)

So my version of FIP is

vs the regular version

Maybe this is silly, but I was a little shocked at how closely they align. If you round my coefficients to the nearest whole number, the equations are identical.

Does FIP work?

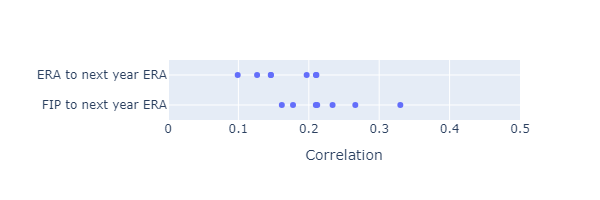
If FIP works as intended, it should have more year-to-year predictive power than ERA. I calculated the correlation between ERA in one year and ERA in the next year with the correlation between FIP in one year and ERA in the next year. I’m comparing

with

Based on year to year correlations from 2015 to 2023, FIP does seem to have better year-to-year predictive power. The plot below shows a 1D scatter plot of the year-to-next-year correlations from 2015 to 2023.

xFIP

If you’ve seen FIP, you may also have come across a related stat called xFIP (the x stands for “expected”). It’s based on a familiar observation. Just like pitchers seem to not have much control over BABIP, they also don’t seem to have much control over their home run to fly ball ratio. xFIP is just like FIP except that it replaces the player’s actual home run total with an expected home run total by replacing their home run to fly ball ratio with the league average ratio:

with

This has always felt a little strange to me. Now xFIP is back to being dependent on fielders and the luck of precisely where balls land.

It’s simple to implement:

league_avg_hr_fb = logs["HR"].div(logs["FB"]).mean()
logs["xHR"] = logs["FB"] * league_avg_hr_fb

X = logs[["xHR", "UBB_HBP", "SO"]].div(logs["IP"], axis=0) # normalize by innings pitched
y = logs["ERA"]
weight = logs["IP"]
xfip_reg = LinearRegression().fit(X, y, sample_weight=weight)

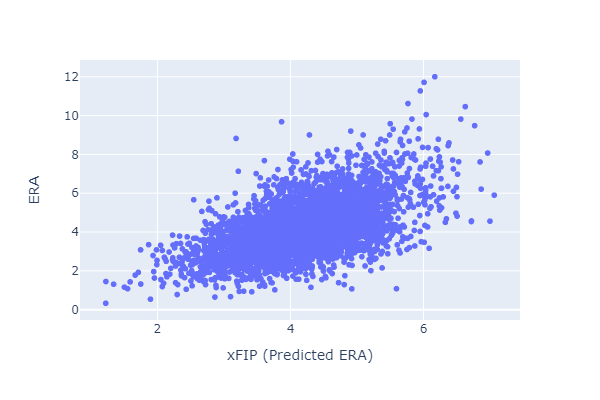
The relationship between (same year) xFIP and ERA seems worse than that between FIP and ERA:

Does xFIP work?

I repeated the above experiments to look at xFIP’s predictive power. 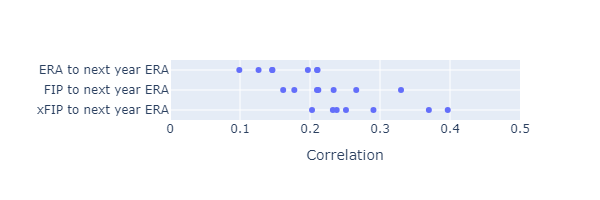xFIP seems to have somewhat more predictive power than FIP or ERA.

How similar is this to real FIP?

At time of writing, I haven’t found a satisfying derivation of the FIP equation. As best I can tell, the coefficients are derived from a type of run value estimate of each possible plate appearance outcome called linear weights. That topic probably deserves a post of its own. However, my method found an equation that’s very similar to the real FIP equation, so maybe it doesn’t matter how it was originally calculated. If two different methods arrive at the same answer, that ought to give us extra confidence in the result.

We’ve made a lot of progress since my first marble machine post!

Major Changes

Here’s an overview of the main changes we made since my last post.

Smaller, Better Marbles

Most obviously, we’ve switched from 3/8” stainless steel balls to 6mm ABS beads. I was skeptical at first, but I now see that this is better for a number of reasons.

Why was I skeptical? I thought that small plastic beads would be too light and would get stuck in the machine, either by static charge or by just not having enough inertia to roll when necessary. Steel ball bearings are sold as machine parts and can be bought with tight tolerances. We were able to get two colors by oxidizing the steel with chemicals. The only plastic balls we could find that came in multiple colors were sold as art supplies or decoration. I thought this would mean they were inconsistent or not perfectly round. This has not been a problem at all. The balls are actually easier to move around by virtue of being lighter. The black and white beads have much better contrast than the oxidized and unoxidized ball bearings.

We’re using a product sold as “undrilled beads”.

Fiber Optic Color Sensing

The machine needs to know what color marbles are to be able to place them in the correct column. We do this with an RGB pixel sensor and an LED for illumination. Fitting the LED/sensor module onto the carriage was awkward and an annoying constraint. We solved this by moving the sensor to the side of the carriage and moving light around using PMMA fiber optic cables. One cable illuminates the marble and the other collects light for the sensor. I’m sort of surprised by how well this works.

It looks cool, too.

Bucket-Style Reservoir

One issue we’d been grappling with is the size of the ball reservoir. If we want to be able to display all possible images, we need at least enough black marbles to fill the whole screen and an equal number of white marbles. Imagine actually trying to draw a full black image with that configuration, though. The stream of marbles is drawn semi-randomly from the reservoir. Hunting for those last few black marble could take a while. If the reservoir can hold three times the number of marbles in the screen, it will still contain one third black marbles even when the screen is all black. That’s a big reservoir, though.

In previous versions, marbles were completely confined to a single plane. To increase the reservoir size without having it dominate the visible surface, we added a big out-of-plane bucket behind the machine.

Smoothly-Curved Elevator Channel

We ran into issues with balls binding in the lower-left corner, where a stepper motor lifts marbles to the top of the machine. Previous versions featured a corner with a polygonal wall. 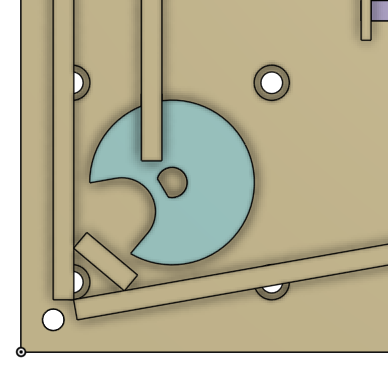This was a simple design achievable with the laser cutter.

The new version has a smooth corner. Also produced using a laser cutter, but a little less obvious.

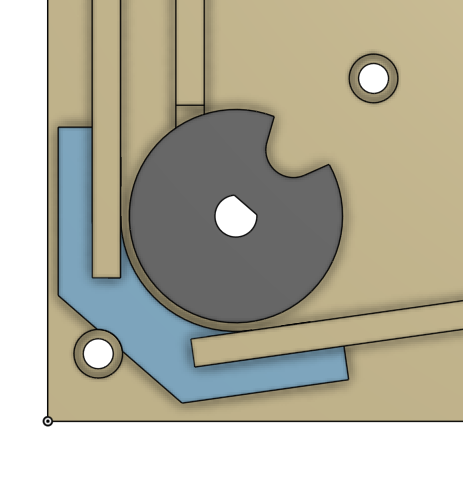
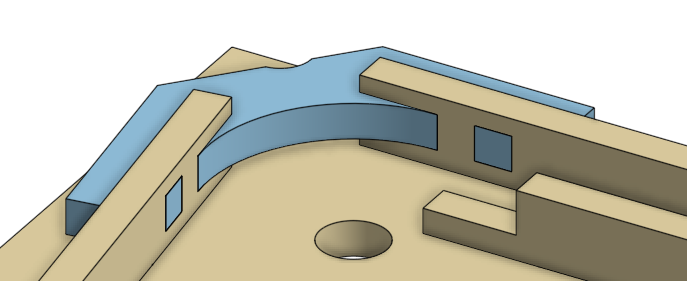
Improved Stepper Driver

In earlier versions of the marble machine, we used simple H-bridge style stepper drivers. They essentially just amplify the output of a digital pin. If, like us, you’re using the GPIO pins of a Raspberry Pi to command the driver, these are terrible. The speed that the pins can be controlled at and the consistency of the timing makes the drive speed low and the motor very noisy.

We changed to a proper CNC control board that reads GRBL G-code. Now, instead of directly controlling the state of every pin, the Pi just sends serial commands saying “go to position 10 mm”.

Getting this working was an ordeal, but was totally worth it. We had to fight to get this working, but now that it is the motion of the carriage and elevator is smooth and fast.

My dad turned 70 this year, so Matt and I decided to make him an old man rocking chair. This project was an adventure. We wasted a lot of perfectly good cherry by repeatedly messing up and/or changing our design. Still, I’m proud of how it came out:

Our inspiration was a beautiful rocking chair we found online: Our starting design closely followed the Masaya chair. We planned to copy most of the details including the bridle jointed rockers, cantilevered armrests, and stretcher-supported seat. As we built, we made some changes. Usually, we plan things out in advance and more or less stick to the plan. This time, we often deferred choices until we were forced to make them. For example, we never had a coherent plan to connect the seat to the stretchers. Ultimately, we avoided the stretchers all together and fastened the seat to the fame with four 3/4” pins. This strategy, driven mostly by laziness and indecisiveness, was both flexible and stressful. I wasn’t truly confident in the project until we clamped up for the last time.

Eventually, we landed on this:

A Botch-Job in Three Acts

We worked on this project over three periods: one in around Halloween, one over Thanksgiving, and one just after Christmas.

Act I: Halloween

This was definitely our spookiest (and least successful) session. Matt and I got together and made doomed pieces for the frame. We cut two rockers, four vertical supports, and three stretchers. Out of the nine pieces we built that weekend, only three made it into the final piece.

The rockers were the most bone chilling part to replace because they were cut from a ridiculously expensive piece of 9” wide 8/4 cherry. I bought a band saw on Craigslist specifically for this project. It’s a cheap 8” Delta benchtop band saw. I drove about an hour to pick it up. The seller turned out to be a pawn shop.

We tried some test cuts and were immediately disappointed. This saw clearly wasn’t powerful enough for 8/4 hardwood and the surface finish was absolutely terrible. We opted instead to cut the rockers using a jigsaw. This was a big mistake. Rocker one looked okay, but while cutting rocker two the blade deflected almost half an inch. We switched back to the band saw to correct the undercut, but the damage was done. We convinced ourselves at the time that thinner rockers would be okay, but I think we both knew the truth.

Act II: Thanksgiving

Over Thanksgiving, we made the seat. We bravely defied typical three act structure, so this session went much better. One contributing factor was a new band saw. Will joined me to drive up toward the New Hampshire border to buy a much bigger and much better 12” Craftsman band saw for only $75. The seller was a nice man who had just finished reffing a soccer game and was not a pawn shop. Here’s Matt using it to cut a part of the seat back:

One aspect of the design that we deferred until the last minute was the woven seat. We bought a thousand feet of black polyester rope and ignored the question until it was time to start winding. The rope came on a massive and intimidating spool. We tested out a few options and dove in. Clamping the seat to a vertical column allowed us to pass the spool back and forth easily. There was so much rope. Eventually, it came together.

Act III: Christmas

The climactic final act. We got together for almost a week after Christmas and finished things up. First order of business: bite the bullet and buy more wood. The new rockers were a huge improvement. It was definitely the right decision to replace them. We also changed the design, replacing the cantilevered armrests with a more symmetrical design and adding overhangs in a few places to visually match the seat. As we clamped the seat to the frame to decide how it would fit, we realized that the stretchers supporting the seat weren’t necessary. Instead, we connected the parts with pins. We finally glued things up at 3 AM on New Year’s Day.

Very happy with how this project turned out. Happy birthday, Dad!