Reinventing the Wheel: Discovering the Optimal Rolling Shape with PyTorch

It is thought that the wheel was invented more than five thousand years ago, yet modern machine learning tools were only developed in the past few decades. We have all wondered about this paradox at some point. How could ancient Sumerian wheel builders have calculated the ideal shape without modern computers and software? We may never know. Luckily, with today's technology, it is relatively easy to rediscover the wheel's optimal shape. I'll show you how I did it.

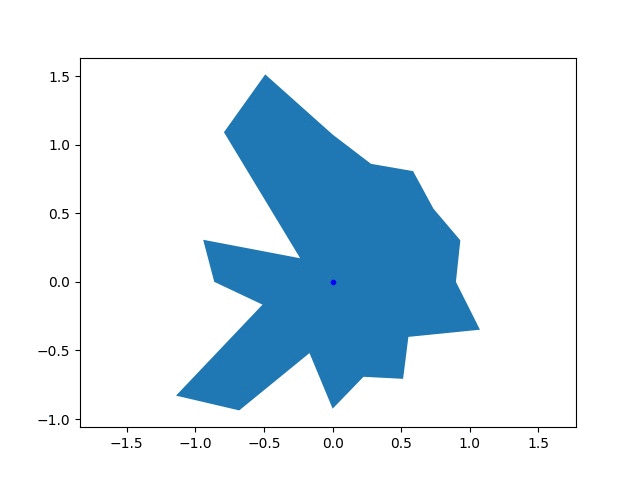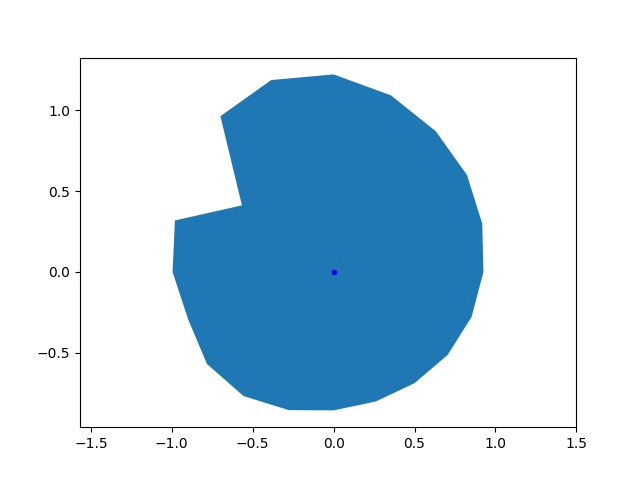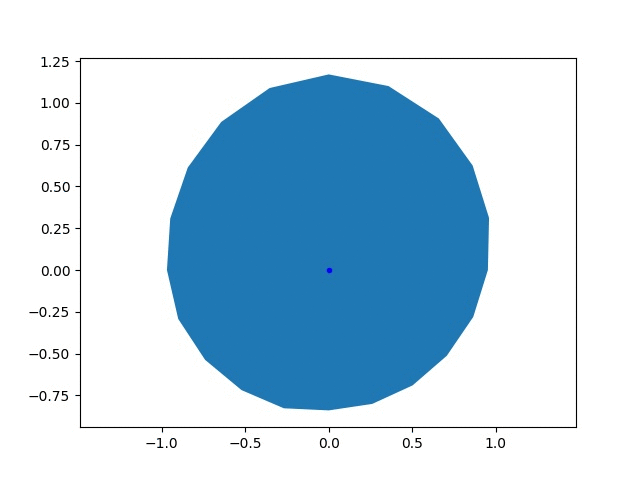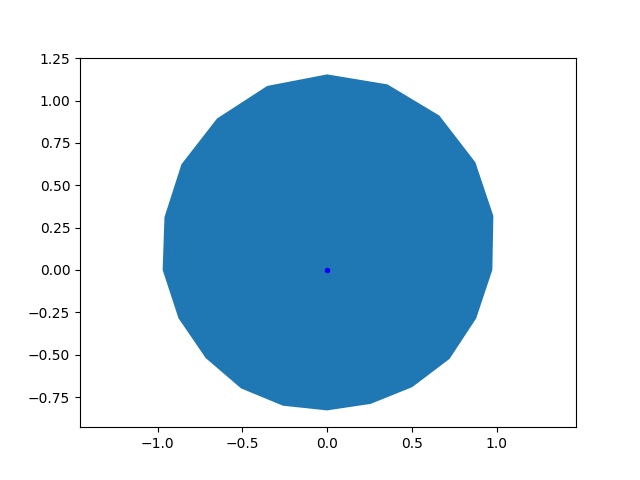
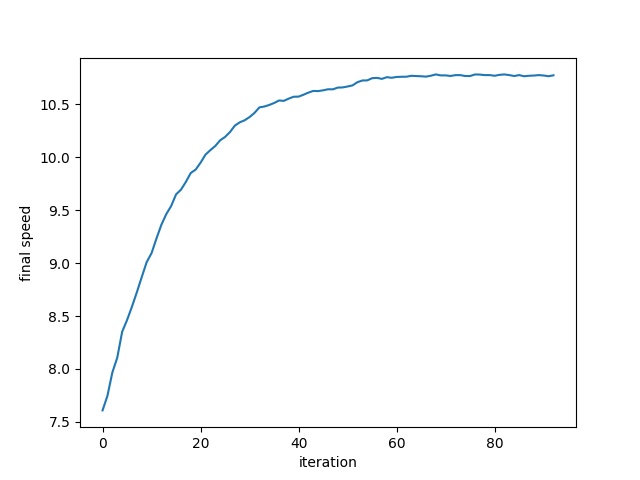
The goal of this goofy project was to find the optimal shape of a wheel, which is probably a circle. I parameterized the wheel as a twenty sided polygon with a variable radius for each vertex, \(r_i\). The performance of the wheel was based on the final speed achieved by an accelerating imaginary car, \(v_f\). The wheel was driven with a constant torque, \(\tau\), and no slipping. I used PyTorch to simulate the effect of a wheel and calculate the gradients in the final speed with respect to the radii, \(\frac{dv_f}{dr_i}\). I used these gradients to update the radii using gradient descent. Above, you can see the shape of an initially randomly generated wheel the wheel evolving, along with the changing objecive function.

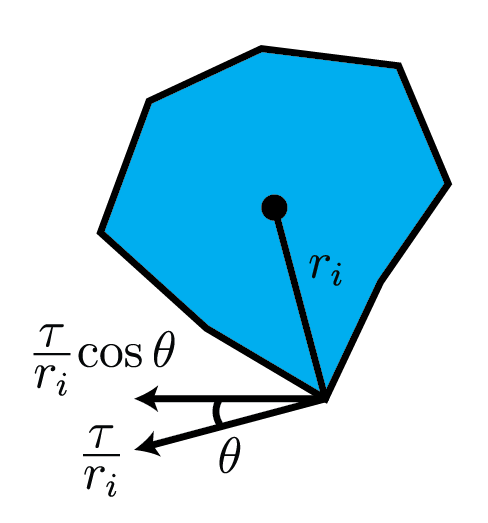
I represented the wheel with a relatively simple model. In each time step, I updated the speed of the car based on the force from the wheel, then rotated the wheel based on the speed. The lowest vertex was touching the ground and was fixed in space. The wheel generated a force on the car \(\tau/r_i\), where \(r_i\) is the radius of the vertex. A component of this force, shown in the diagram below, accelerated the car and increased its speed.

Next, I think it would be fun to try surfaces that aren't flat. If I used that rolling square surface, would the optimal shape be a square?

import torch
import numpy as np
import matplotlib.pyplot as plt

n = 20 # number of wheel points
n_steps = 1000 # number of steps to test the wheel performance
#radii = torch.tensor([2.] + [1.] * (n-1), requires_grad=True) # init wheel radii with one bump
radii = torch.tensor(np.random.normal(1., .4, size=n).astype(np.float32), requires_grad=True) # init random wheel point radii
dtheta = 2. * np.pi / n # angle between wheel points
thetas = torch.arange(0,2*np.pi, dtheta) # list of wheel point angles
dt = 0.1 # time step for dynamics
torque = 1. # torque on the wheel
mass = 10. # mass of the car
gravity = .1 # acceleration due to gravity

# finds the final speed of the wheel from radii
def test_wheel(radii):
    # normalize the radii so that changing the size has no effect
    norm_radii = radii / torch.mean(radii)

    # find the coordinates of the wheel points
    vertex_positions = wheel_coordinates(norm_radii)

    speeds = torch.zeros(n_steps) + 1. # speed of the cart after each step
    angle = 0

    # simulate the wheel performance
    for i in range(1,n_steps):
        # find pivot properties
        pivot_index = torch.argmin(vertex_positions[:,1])
        pivot_radius = norm_radii[pivot_index]
        pivot_vector = vertex_positions[pivot_index]
        pivot_angle = torch.atan2(pivot_vector[1], pivot_vector[0])

        # don't use pivot angle, just take the height of the pivot
        
        # calculate force at the pivot point
        force = torque / pivot_radius

        #force_gravity = gravity * mass * torch.sin(pivot_angle + np.pi/2)
        force_gravity = 0

        # calculate the component of pivot force that pushes the car forward
        force_component = torch.cos(pivot_angle + np.pi/2)

        # calculate the new speed of the car and the rotational speed of the wheel
        speeds[i] = speeds[i-1] + ((force * force_component + force_gravity) * dt / mass)
        rotational_speed = speeds[i] * force_component / pivot_radius
        
        dangle = rotational_speed * dt
        angle += dangle
        
        # rotate the wheel
        vertex_positions = rotate(vertex_positions, dangle)

    #print(angle)
    return speeds

def draw_wheel(vertex_positions):
    xs, ys = vertex_positions.transpose(0,1).detach().numpy()
    plt.scatter(xs, ys)
    
# returns a rotation matrix
def rotation_matrix(theta):
    return torch.tensor([[torch.cos(theta), torch.sin(theta)],[-torch.sin(theta), torch.cos(theta)]])

# returns the wheel coordinates based on the radii
def wheel_coordinates(radii):
    vertex_positions = (radii.unsqueeze(1) * torch.cat((torch.cos(thetas.reshape((-1,1))),torch.sin(thetas.reshape((-1,1)))), 1))
    return vertex_positions

# returns a rotated set of vertex positions
def rotate(vertex_positions, theta):
    rot_matrix = rotation_matrix(theta)
    vertex_positions = torch.matmul(rot_matrix, vertex_positions.transpose(0,1)).transpose(0,1)
    return vertex_positions

# list to keep track of objective progress
final_speeds = []

# objective plot
fig_obj = plt.figure()
ax_obj = fig_obj.add_subplot(111)
ax_obj.autoscale(enable=True, axis="y", tight=False)
ax_obj.set_xlabel("iteration")
ax_obj.set_ylabel("final speed")

li_obj, = ax_obj.plot(final_speeds)

# radii plot
fig_rad = plt.figure()
ax_rad = fig_rad.add_subplot(111)

li_rad, = ax_rad.plot(radii.detach().numpy())

# wheel shape plot
fig_wheel = plt.figure()
ax_wheel = fig_wheel.add_subplot(111)
ax_wheel.set_aspect('equal', 'datalim')

vertex_positions = wheel_coordinates(radii)
vertex_xs, vertex_ys = vertex_positions.transpose(0,1).detach().numpy()
li_wheel, = ax_wheel.fill(vertex_xs, vertex_ys)
li_hub, = ax_wheel.plot(0, 0, 'b.')

fig_obj.canvas.draw()
fig_rad.canvas.draw()
fig_wheel.canvas.draw()
plt.show(block=False)

lr = 0.03 # learning rate
for i in range(100000):
    # simulate wheel
    speeds = test_wheel(radii)

    # cost
    final_speeds.append(speeds[-1])
    cost = -speeds[-1]

    # calculate gradients
    cost.backward(retain_graph=False)

    # gradient descent
    with torch.no_grad():
        radii -= radii.grad * lr
        radii.grad = None

    # update plots
    li_obj.set_data(range(len(final_speeds)),final_speeds)
    li_rad.set_ydata(radii.detach().numpy())

    ax_obj.relim()
    ax_obj.autoscale_view()


    vertex_positions = wheel_coordinates(radii)
    vertex_xs, vertex_ys = vertex_positions.transpose(0,1).detach().numpy()
    ax_wheel.clear()
    ax_wheel.set_aspect('equal', 'datalim')
    ax_wheel.fill(vertex_xs, vertex_ys)
    ax_wheel.plot(0, 0, 'b.')

    fig_obj.canvas.draw()
    fig_rad.canvas.draw()
    fig_wheel.canvas.draw()

    fig_wheel.savefig("vid_3/wheel_{i}.jpg".format(i=i))
    fig_obj.savefig("vid_3/obj.jpg")

You've Reached the Center of the Internet

It's a blog

Reinventing the Wheel: Discovering the Optimal Rolling Shape with PyTorch